Campo magnético terrestre

Término(s) similar(es): campo geomagnético.

Definición:

El campo geomagnético es el campo de fuerza magnética que rodea la Tierra. Se atribuye al efecto combinado de la rotación planetaria y el movimiento del hierro fundido en el núcleo del planeta.

Las brújulas son instrumentos que se alinean con los polos magnéticos de la Tierra y que se han utilizado en navegación durante siglos. Algunas aves (sobre todo las migratorias) y otros animales se sirven del campo geomagnético para orientarse.

Fuente: GreenFacts

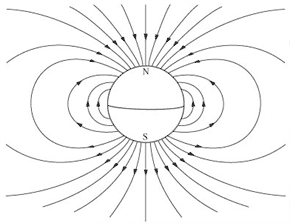
El campo magnético terrestre es el resultado del núcleo de hierro de nuestro planeta al girar, lo que da como resultado que nuestro planeta, y muchos otros cuerpos como el sol y planetas, sean como imanes gigantes; gracias a este campo tenemos la magnetosfera, eso es algo así como una burbuja que rodea a la tierra y que sirve como escudo contra los vientos solares (desvía la mayor parte de ellos) y nos proeje de radiaciones cósmicas y partículas solares nocivas. También el campo magnético es aprovechado por muchas criaturas que utilizan el campo magnético para moverse por el planeta, incluyendo a los seres humanos.

otro. 

Campo eléctrico. Líneas de campo Una carga eléctrica puntual q (carga de prueba) sufre, en presencia de otra carga q1(carga fuente), una fuerza electrostática. Si eliminamos la carga de prueba, podemos pensar que el espacio que rodea a la carga fuente ha sufrido algún tipo de perturbación, ya que una carga de prueba situada en ese espacio sufrirá una fuerza. La perturbación que crea en torno a ella la carga fuente se representa mediante un vector denominado campo eléctrico. La dirección y sentido del vector campo eléctrico en un punto vienen dados por la dirección y sentido de la fuerza que experimentaría una carga positiva colocada en ese punto: si la carga fuente es positiva, el campo eléctrico generado será un vector dirigido hacia afuera (a) y si es negativa, el campo estará dirigido hacia la carga (b): Campo eléctrico creado en el punto P por una carga de fuente q1 positiva (a) y por una otra negativa (b). El campo eléctrico E creado por la carga puntual q1 en un punto cualquiera P se define como: donde q1 es la carga creadora del campo (carga fuente), K es la constante electrostática, r es la distancia desde la carga fuente al punto P y ur es un vector unitario que va desde la carga fuente hacia el punto donde se calcula el campo eléctrico (P). El campo eléctrico depende únicamente de la carga fuente (carga creadora del campo) y en el Sistema Internacional se mide en N/C o V/m. Si en vez de cargas puntuales se tiene de una distribución contínua de carga (un objeto macroscópico cargado), el campo creado se calcula sumando el campo creado por cada elemento diferencial de carga, es decir: Esta integral, salvo casos concretos, es difícil de calcular. Para hallar el campo creado por distribuciones contínuas de carga resulta más práctico utilizar la Ley de Gauss. Una vez conocido el campo eléctrico E en un punto P, la fuerza que dicho campo ejerce sobre una carga de prueba q que se sitúe en P será: por tanto, si la carga de prueba es positiva, la fuerza que sufre será paralela al campo eléctrico en ese punto, y si es negativa la fuerza será opuesta al campo, independientemente del signo de la carga fuente. En la siguiente figura se representa una carga fuente q1 positiva (campo eléctrico hacia afuera) y la fuerza que ejerce sobre una carga de prueba q positiva (a) y sobre otra negativa (b): Fuerza que un campo eléctrico E ejerce sobre una carga de prueba q positiva (a) y sobre otra negativa (b). El campo eléctrico cumple el principio de superposición, por lo que el campo total en un punto es la suma vectorial de los campos eléctricos creados en ese mismo punto por cada una de las cargas fuente. Líneas de campo El concepto de líneas de campo (o líneas de fuerza) fue introducido por Michael Faraday (1791-1867). Son líneas imaginarias que ayudan a visualizar cómo va variando la dirección del campo eléctrico al pasar de un punto a otro del espacio. Indican las trayectorias que seguiría la unidad de carga positiva si se la abandona libremente, por lo que las líneas de campo salen de las cargas positivas y llegan a las cargas negativas: Las líneas de campo creadas por una carga positiva están dirigidas hacia afuera; coincide con el sentido que tendría la fuerza electrostática sobre otra carga positiva. Además, el campo eléctrico será un vector tangente a la línea en cualquier punto considerado. Líneas de campo causadas por una carga positiva y una negativa. Las propiedades de las líneas de campo se pueden resumir en: El vector campo eléctrico es tangente a las líneas de campo en cada punto. Las líneas de campo eléctrico son abiertas; salen siempre de las cargas positivas o del infinito y terminan en el infinito o en las cargas negativas. El número de líneas que salen de una carga positiva o entran en una carga negativa es proporcional a dicha carga. La densidad de líneas de campo en un punto es proporcional al valor del campo eléctrico en dicho punto. Las líneas de campo no pueden cortarse. De lo contrario en el punto de corte existirían dos vectores campo eléctrico distintos. A grandes distancias de un sistema de cargas, las líneas están igualmente espaciadas y son radiales, comportándose el sistema como una carga puntual.